La tercer prueba será el miércoles 27 a las 9:15hs
El examen será el Lunes 16 a las 13:00hs
Adjunto material del módulo.
viernes, 22 de noviembre de 2013
martes, 29 de octubre de 2013
[FF4] USO DE XO
Clase 29/Oct
Con el uso de las XO, buscar y anotar en cuaderno los conceptos de:
- Estadística
- Población
- Muestra
- Muestreo
- Frecuencia relativa y absoluta
- Moda
- Mediana
- Media Aritmética
- Frecuencia relativa acumulada y frecuencia absoluta acumulada.
Notas:
9 cumplidas = 12 puntos
7 u 8 cumplidas = 9 a 11 puntos
6 cumplidas = 8 puntos
5 cumplidas = 7 puntos
4 o menos cumplidas = 1 a 6 puntos.
lunes, 28 de octubre de 2013
[DA1] Uso de XO
Clase 28/Oct.
Primera hora de clase:
Buscar y anotar en cuaderno una idea resumida de:
- Números enteros y regla de los signos.
- Concepto de trigonometría y razones trigonométricas.
Segunda hora de clase:
Búsqueda más libre sobre temas de taller, siguiendo ciertas ideas generales como: Tipos de telas del mercado, nombres y ubicación de locales de venta en Montevideo, diseño y patrones, ect.
Objetivo:
Para que una búsqueda en Internet sea eficiente, amerita poseer ciertas conductas para con los motores de búsqueda del mercado. Ésta clase se destina precisamente a que los estudiantes busquen información con la guía del docente.
Páginas encontradas que el alumnado podrá encontrar de utilidad:
- A Todo Trapo Telas (venta de telas en Uruguay)- Link
- Tienda Montevideo (Telas y cortinas)- Link
- Telas Mary (Venta de telas en Argentina)- Link
- TecnologíaTextil (Empresa textil en Perú)- Link
- Patrones de diseño:
- Introducción a la costura y patrones al final (PDFs):
- Maquina de coser- Link
- Patrones y diseño para mascotas- Link
viernes, 16 de agosto de 2013
[FF4]-[DA1]
TEOREMA DE PITÁGORAS
- Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º.
- En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos.
Sabido ésto,
Enunciado del Teorema de Pitágoras:
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
AC = cateto = b
BC = hipotenusa = a
La expresión matemática que representa este Teorema es:
Ejemplos:
1)
***
2)
Usos, ejercicios de razonamiento:
1)
¿Cómo podríamos calcular cuánto mide la muralla?
Solución:
2)¿A qué distancia de la tierra se encuentra el barco si se sabe que la distancia del barco a la parte superior del faro es 25 metros y, además, está 20 metros sobre el nivel del mar?
martes, 30 de julio de 2013
[DA1]Rectas y puntos
¿Qué es un punto?
El punto es el elemento base
de la geometría, porque con él determinamos las rectas y los planos.
Podemos definirlo también como la intercesión de dos lineas,sirve para indicar
una posición y no tiene dimensión.
¿Qué es una recta?Una recta es
una sucesión ininterrumpida de puntos, dos puntos determinan una recta, tienen
una dimensión, la longitud.
Tipos de rectas:
- Recta:
La recta propiamente dicha se caracteriza por que los puntos que la forman están en la misma dirección. Tiene una sola dirección y dos sentidos. No se puede medir. - Semirrecta:Es linea
recta que tiene origen pero no tiene fin, tiene sólo un sentido,y no se
puede medir.
- Segmento:
Un segmento es una linea recta que tiene principio y fin, un segmento se puede medir.
Posiciones de las rectas:
- Dos rectas
son paralelas: si no tienen ningún punto en común o tienen todos los puntos en
comun.
- Dos rectas
son secantes: cuando tienen un punto en común
- Dos rectas
son perpendiculares: cuando al cortarse forman cuatro ángulos
rectos
Construcción
Paralelas
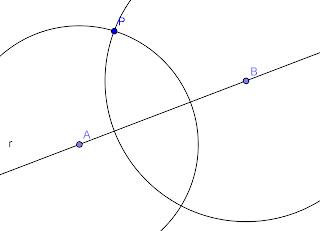
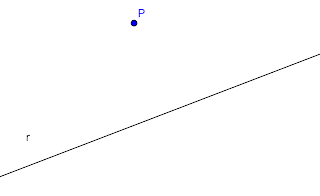
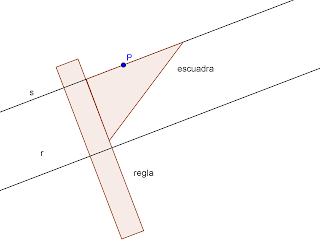
Supongamos que queremos construir una recta paralela a la recta rque pase por el punto P.
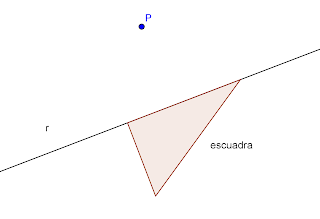
Apoyamos uno de los catetos de una escuadra en la recta r.
Sobre el otro cateto apoyamos una regla.

Deslizamos la escuadra sobre la recta, hasta que el cateto que se encontraba sobre la recta quede sobre el punto P.
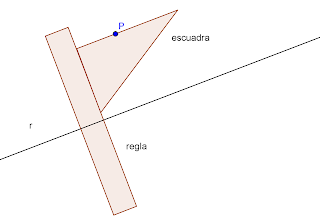
Trazamos la rectas s paralela a r.

Apoyamos uno de los catetos de una escuadra en la recta r.

Sobre el otro cateto apoyamos una regla.

Deslizamos la escuadra sobre la recta, hasta que el cateto que se encontraba sobre la recta quede sobre el punto P.

Trazamos la rectas s paralela a r.

Perpendiculares
Con regla y compás
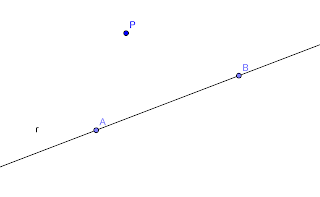
Supongamos que tenemos una recta r y un punto P y queremos trazar una recta perpendicular a r que pase por el punto P.
Marcamos dos puntos A y B sobre la recta r.
 Luego trazamos dos arcos de circunferencias con centros en A y B y que pasen por el punto P, tratando que los arcos se intersecten también del otro lado.
Luego trazamos dos arcos de circunferencias con centros en A y B y que pasen por el punto P, tratando que los arcos se intersecten también del otro lado.
Marcamos el punto de intersección Q y trazamos la recta s de tal manera que pase por los puntos P y Q.
Fuente: http://puntoyrecta.blogspot.com
Video:
domingo, 14 de julio de 2013
[FF3] Resumen del Trayecto 2 Módulo III
Como se habrán dado cuenta, termino el módulo 5.
Hago y comparto un resumen de los temas dados, o que debí dar y por razones de tiempo no fue posible.
El Trayecto 2 Módulo III se divide en tres grandes puntos:
Hago y comparto un resumen de los temas dados, o que debí dar y por razones de tiempo no fue posible.
El Trayecto 2 Módulo III se divide en tres grandes puntos:
- POLINOMIOS,
- ECUACIONES Y SISTEMAS DE ECUACIONES y
- SISTEMAS DE COORDENADAS Y FUNCIONES
A continuación los links a tres PDFs con lo temas ya mencionados.
Es de aclarar que, a quienes vayan a seguir estudiando, y espero que todos, o a quienes tengan que dar examen de la materia, estos temas son de suma prioridad.
Saludos y ante cualquier duda a las órdenes.
Saludos y ante cualquier duda a las órdenes.
lunes, 17 de junio de 2013
miércoles, 22 de mayo de 2013
[FF3]
ECUACIONES!
Videos encontrados donde explica de forma similar a lo dado en clase de Mecánica FF3
martes, 7 de mayo de 2013
[DA1] Escala
Conversiones de medidas
Para el manejo y manipulación de las escalas, tema central de la actualización, será necesario conocer y repasar conversiones de medidas.
Para ello comparto una imagen con la tabla trabajada en clase y un vídeo que explica lo mismo.
ESCALA
Definición
La escala es la relación matemática que existe entre las dimensiones reales y las el dibujo que representa la realidad sobre un plano o un mapa. Es la relación de proporción que existe entre las medidas de un mapa con las originales.
Tipos de escalas
Existen tres tipos de escalas llamadas:
Escalas
de ampliación
Escalas
de reducción
10:1
5:1 2:1
1:2
1:5 1:10
50:1
20:1
1:20
1:50 1:100
1:200
1:500 1:1000
1:2000
1:5000 1:10000
Escala
natural
1:1
Paso de medida Reales a escala
Si llamamos
- E (escala) o [M (a su numerador) y N (el divisor de la escala)]
- P (dimensión en el papel)
- T (dimensión real)
Entonces:
Definición
La escala es la relación matemática que existe entre las dimensiones reales y las el dibujo que representa la realidad sobre un plano o un mapa. Es la relación de proporción que existe entre las medidas de un mapa con las originales.
Tipos de escalas
Escalas
de ampliación
|
Escalas
de reducción
|
10:1
5:1 2:1
|
1:2
1:5 1:10
|
50:1
20:1
|
1:20
1:50 1:100
|
1:200
1:500 1:1000
|
|
1:2000
1:5000 1:10000
|
|
Escala
natural
|
1:1
|
Paso de medida Reales a escala
Si llamamos
- E (escala) o [M (a su numerador) y N (el divisor de la escala)]
- P (dimensión en el papel)
- T (dimensión real)
Entonces:
Ejemplo:
jueves, 18 de abril de 2013
lunes, 8 de abril de 2013
[FF3]-[DA1]
A continuación: material claro de fracciones y ejercicios extra a la clase, para quienes quieran seguir practicando.Material de FRACCIONES
Ejercicios con Soluciones
[FF3]
Programa de Mecánica Automotriz- FF3
PLANIFICACIÓN ANUAL:
(Mecánica automotriz Trayecto 2 Módulo III)
4hs Semanales
1h Integrado a taller
1h Integrado a taller
2hs Coordinación
Aprox. 36 Semanas de Clase (144 hs): 16 Semanas Módulo III; 20 Semanas Módulo IV
MÓDULO III:
Marzo
(3 Sem.)
|
Repaso Conjuntos Numéricos.
Operaciones con enteros y fracciones. Noción de números irracionales.
Introducción a funciones. Concepto, tipos y aplicaciones simples.
|
Abril
(4 Sem)
|
Repaso de funciones.
Despeje de incógnitas.
Caso de Monomios y polinomios.
Identificación de grados y polinomios reducidos.
|
Mayo
(5 Sem)
|
Operaciones con polinomios (Suma, resta y multiplicación)
Escrito (8/05/2013)
Ecuaciones de primer grado: y=ax+b
Gráfica de soluciones.
Sistema de ecuacione, resolución por igualación, sustitución y eliminación. (2 sem.)
|
Junio
(4 Sem)
|
Uso de gráficas, conjunto de soluciones.
Coordenadas de un punto.
Pasaje de fórmula a gráfica y viceversa.
Aplicaciones a problemas concretos.
Escrito (26/06/2013)
|
Vacaciones de julio (1/07 – 14/07)
MÓDULO IV:
Julio
(2 1/2 Sem)
|
Clasificación de polígonos
Fórmulas de Áreas y Volúmenes de polígonos y poliedros. Ejemplos.
|
Agosto
(4 1/2 Sem)
|
Triángulos. Clasificación y rectas y puntos notables.
Triángulos rectángulos.
Teorema de Pitágoras, fórmula y aplicación.
Medida de ángulos; sexagesimal y decimal. Uso de calculadora cinetifica.
Escrito (30/08/2012)
|
Septiembre
(4 Sem)
|
Trigonometría (razones): Seno, Coseno y Tangente.
Relaciones entre razones trigonométricas.
Aplicaciones.
|
Octubre
(4 1/2 Sem)
|
Escrito (02/10/2013)
Uso de estadística.
Población y muestra.
Frecuencia absoluta y frecuencia relativa.
Ejemplos.
|
Noviembre
(4 1/2 Sem)
|
Frecuencia Absoluta y relativa acumulada.
Aplicaciones concretas.
Gráficas.
Media y mediana.
Escrito (29/11/2013)
|
Suscribirse a:
Comentarios (Atom)